星や宇宙はつかみどころがないのですが、電卓で計算してみると、すごいという感じがつかめます。
人工衛星もお月さまも、宇宙第一速度で釣り合って回っている
月や人工衛星がずっと回っているのは、外に飛び出そうとする遠心力をつける「速度」と、地球に引き戻そうとする「重力」が釣り合っている状態です。
ISS宇宙ステーションが落ちてこないのは、ISSの動く速さと地球がISSを引っ張る重力が釣り合っているということですね。
地上でものを投げると、放物線運動をして地面に落ちますが、スピードを上げていくと段々遠くに飛んで、より遠くの地面に落ちますが、さらにスピードを上げると、ISSのように地球の周りを回り続ける状態になり、さらにそれ以上にスピードが速くなると、宇宙のどこかへ飛んで行ってしまいます。

その釣り合った状態の物体の速度は約7.8km/秒という速度で、それが「第一宇宙速度」で、これ以上の速度であれば、地球から離れて飛んでいきます。
ISS(国際宇宙ステーション)は第一宇宙速度の7.8km/s近くの速さで飛んでいるので、地球に落ちてこないし、遠くへ飛んでいってしまうことはない … という釣り合った状態になっています。
この7.8km/sを電卓を使って時速になおすと 7.8×60(秒)x60(分)で、約28,000km/h と非常に速いスピードであることに驚くと思いますので、電卓をたたいてみてください。
ちなみに、地表の音速は常温では 340m/秒程度で、ジェット機がこのスピードを超えるときに大きな衝撃はが出るので、「音速の壁を破る」という言い方をされますが、この秒速を時速にすると、340mx60秒x60分=1224kmということなので、ISSやロケットの速度は桁違いに速いのです。
(参考) 宇宙に飛び出すための速度には、地球の引力に打ち勝つための 第一宇宙速度(7.8km/s)のほかに、地球の重力を振り切ってお月さんまで行く速度(第2宇宙速度:約11.2km/s)や、太陽の重力を振り切る速度(第3宇宙速度:約16.7km/s)などがあります。
地球も地球に住む人も速い速度で太陽を回っています
太陽の引力と地球の周回速度が釣り合っていて、地球はその軌道を外れないのですが、太陽までの距離は約15,000万km(一億5千万キロ)なので、1年で太陽がほぼ円軌道の一周をまわるとすると、円周率をπとすると、 2πrが円周の距離なので一年間ですので、2xπx15000000/(24x365)≒107500km/h となり、秒速にすると、約29.9km/s という、すごいスピードで動いています。(これを公転スピードといいます)
実際に天体は円軌道でないので、この計算では若干の誤差がありますが、おおよその数字がイメージできれば、そのスピードや大きさをイメージできるでしょう。
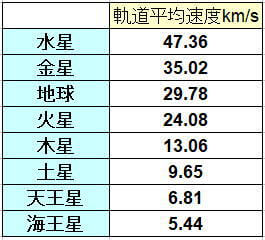
惑星の動くスピードについては理科年表に載っていて、それは次のような数値です。上のアバウトな計算数字でも、当たらずとも遠からずですね。
さらに地球は自転しています。
地上の回転速度は、赤道付近のスピードが最も速く、北極・南極では、1日かかって回れ右して同じところに向くだけという超スロースピードということですが、地球上のどこにいても、そのスピードを感じることはありませんね。
この赤道での速度ですが、赤道半径6378kmとして、1日に円周の距離を動くので、2xπx6378÷24≒1670km/h で秒速では460m/s ですから、赤道にいる人は、地上の音速よりも速いスピードで動いているのですが、周り全部が地球と一緒に動いているので、自転スピードも公転スピードも感じませんし、音速の壁も関係しません。
日本の場合は、北緯35度あたりにあるので、赤道の速さよりも遅くなっていますね。 関数電卓を使って、半径を 6378xcos35≒5224km として同様に計算すると、日本にいても、380m/sぐらいの速さで動いているということですね。
その他の身近な数値を加えて、いろいろな速度の比較表をつくってみました。
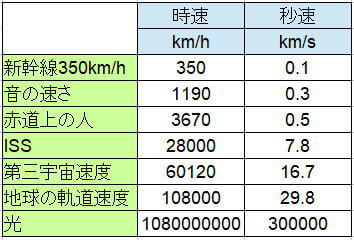
ここで見るように、光は桁違いに速いということが数字でわかります。
ここにある第三宇宙速度とは、太陽の引力圏を抜けるために必要な速さですが、それよりも、太陽を回る地球の公転速度が早いのにびっくりしませんか?
これらの数字は、結構アバウトですが、これも、自分で書き出してみると、自然の凄さが実感できます。
第3宇宙速度を超えて飛んでいる「ボイジャー」
1977年にアメリカが打ち上げたボイジャー(1・2号)は、第3宇宙速度を得て、40年以上かかって、ようやく太陽の重力圏を脱して飛んでいっています。
時速では、第三宇宙速度の 16.7(km/s)x60(秒)x60(分)=60200(km/h)以上の速度で宇宙空間を飛んでいるのです。
このように、時速と秒速のように、単位を変えると感じ方が変わりますが、ただ、光の速さは30万km/sですので、この世で最も早いボイジャーでも、光速の 1/17600 の速さですから、いかに光速がの凄さに驚かされます。
お月さんまでの距離は約38万km、それをロケットで飛ぶと

地球の赤道を一周すると、先ほど出てきた式で、その距離は約4万kmですが、月の半径は1760kmですから、2xパイx半径 を計算してみると、月の赤道を1周すると約11000kmになります。
一番近い天体の「月」ですが、地球から380000キロも離れたところにあります。そして、月の裏側を見せないように、一日にほぼ1回自転しながら地球に対する公転をして、さらに太陽の周りを、1年かけて公転しています。
この「月」も、地球の引力に釣り合うスピードで地球の周りを回っていますが、ほぼ同じ面を地球に向けていますので、速さは感じませんが、非常に速い速度で動いています。
つまり、月は38万km離れて地球を1周しているので、1日の移動距離は 2x円周率x38万km≒239万km で、軌道のスピードは、239万km÷60秒÷60分÷24時間≒27.6km/s となり、これもすごいスピードです。
そこで計算上ですが、地球から38万km向こうのお月さんまで、第二宇宙速度11.2km/sで飛んでいくと、380000(km)÷11.2(km/s)÷60(秒)÷60(ふん)≒9.5(時間)という距離ですが、しかし、実際にアポロ11号が月に行ったときの記事によると、地球脱出の加速と着陸のための減速が必要なので、行く時だけでも、実際には102時間(4日以上)かかっていたようです。
 (NASAの写真:WEBより)
(NASAの写真:WEBより)
現在でも、アポロ宇宙船が月に設置したこの装置で、月までの距離が正確に測定されています。
もちろん、不安定な軌道を描いていることもわかっているので、数字がわかっても、絶えず変動しているという、単純なものではないようですが。
その測定によると、月は、地球の潮汐などの影響で次第に回転が鈍くなっているようで、そのために求心力(相互の引力)が少なくなって、月までの距離が、平均毎年5㎝ほど遠くなっていっているというのです。
月は地球の一部が弾き飛ばされた … という仮説が有力です。 そうなると、大昔の月は地球に近くにあったので、見かけの大きさはもっと大きく、周回速度も早かったのですが、このあたりの計算は少し難しそうなのと実際の月の成因もわからないので割愛しますが、概算であれば計算してみると面白いですよ。
隣の恒星「プロキシマ・ケンタウリ」に行くには
太陽までロケットで行くことは無理で、もしも行けたとしても、重力に引っ張られて帰れないし、焼け焦げてしまって、帰ってくることができません。
現在、アメリカが太陽に向かって探査機を飛ばしていて、太陽風などを観測しているようですが、早く結果が知りたいですね。
第一宇宙速度で太陽に向かって飛んでいけば、地球の重力を振り切った後は、太陽の引力で引き寄せられるのですが、ここで、太陽までの距離が150000000kmで第一宇宙速度が28000km/hとすると、定速で計算すれば 200日強で太陽に到着するといっても、もっと早くに焼けてしまいそうです。
恒星に向かうのは問題があるのですが、机上での計算はできます。 ここでは、太陽より遠くにある恒星への旅を計算値でイメージしてみましょう。
太陽系に最も近い恒星は「プロキシマ・ケンタウリ」で、南十字星の近くのケンタウルス座にあり、日本から見ることは出来ませんが、4.25光年のところにある「地球に最も近い恒星」です。
光が毎秒30万km進んで4年以上もかかるのですから、人類最速のボイジャーの20km/秒の速度でも、 300000÷20=15000で、光の15000倍もかかります。 直進するとして、片道だけで6万年以上もかかるという計算になります。
SFなどで出てくる「ワープ」などの特殊なからくりがなければ、有人飛行は考えられませんし、もちろん、太陽と同じように「燃えている」のですから、近くには行けないのですが、計算をやって現実と対比させると、親密さとともにいろんなイメージが膨らんできませんか?
4.25光年の測定はどのようにする?
現在の天文学では、「プロキシマのように近い星は比較的簡単に距離がわかる」といいます。
星の位置は変わらないとすれば、近い星を半年間観測して、地球の公転半径と年周視差で計算できます。
それによって、現在では「±0.01光年の誤差でプロキシマまでの距離4.25光年は正しい」ということのようです。
この「誤差0.01光年」というのは 光速30万km/秒 から計算して、kmに換算すると300000(km/h)x60(秒)x60(分)x24(時間)x365(日)x0.01=94,608,000,000kmにもなります。
地球の直径をおよそ13000kmとすると、地球約700万個以上を並べた距離の誤差があるのですが、これは数字の持つ魔術があって、「±0.01光年の誤差で … 」といわれるのと、地球700万個の誤差といわれるのでは、まったく感じ方が違ってくるのですが、私は、むしろ、この「すごい距離」が角度の測定から求められていることに驚いています。
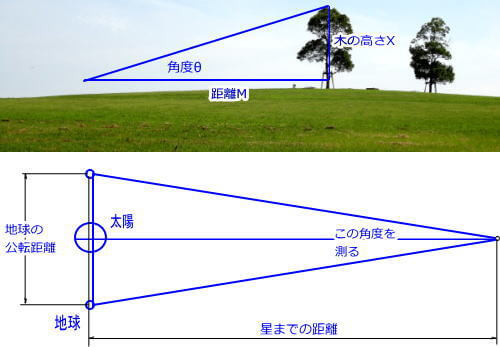
このような方法で年周視差から三角法で比較的近い星までの距離を求めるのですが、(概数計算で)地球の公転距離が3億km、星までの距離が4.25光年≒40兆km とすると、それを割ると 0.0000075 という数字になります。
例えば角度が1度のタンジェントの値は0.175程度の値ですので、0.0000075は、角度1度の1/4000の値を測定していることです。
その測定値の0.0000075が0.0000074になっただけでも、5400万kmの違いが出るという数字です。 そうなると、地球の4000個分以上の誤差になるというのですが、この数字を、角度測定で求められている事自体が「すごいこと」としか言いようがありません。
天文学的な数字
このように、桁数の多い、ものすごい大きな数字を「天文学的」と表現されます。
数字が示されても実感がわかないですが、それでも、数字を見るか見ないのでは感じ方が違います。
 オリオン座と冬の大三角
オリオン座と冬の大三角
近年、このオリオン座の左上の「ペテルギウス」が減光しているという話題があります。 だから、「消滅寸前ではないか … 」というのですが、このペテルギウスまでの距離は、約640光年といいますので、640年前の光がいま地球に届いているということですが、ひょっとすると、すでに消えてしまっているかもしれないものですが、光の速さを超えて調べることができないので、誰にも行方が分からないのですが、何よりも、そんな遠くの光が届くのが不思議です。
宇宙には光を遮るものがほとんどないというのですが、宇宙のすごさにも驚きます。
宇宙の大きさ138億光年は何Km?
宇宙関連の数字は遥かに大きく、例えば、宇宙の端までは138億光年もの距離があるといいます。
この数字は年を追うごとに変わってきています。
50年ほど前には、宇宙の大きさは100億光年程度と学んだように記憶していますが、遠くの星を観測すると、遠いほど速いスピードで遠ざかっているようで、さらなる発見があるごとに大きくなるのですが、宇宙が小さくなることは当面はないようです。
それはともかく、仮に、宇宙の果までを138億光年をkmにすると、光速30万km/sx60(=分)x60(=時間)x24(=日)x365(=年)x138億ですので、数字で書くと、1,305,590,400,000,000億km の距離というのが関数電卓で計算出来ます。
1.3…e23 という表示になっているかもしれませんが、これは、1のあとに数字が23個も付く130559040000000000000000km という数ですが、これを電卓で計算するのに、一連作業を含めて1分間要したのなら、その間に、光は30万x60(秒)=180000000kmも進んでいることになります。
宇宙の数字はロマン?
今、宇宙物理学の研究者は、ビッグバンのときに生じたとされる「重力波」を見つけることに躍起となっているらしく、その計測には、0.000000000001m、つまり「ピコメートル単位」の測定精度が必要と見積もられています。(ちなみに、水の分子の大きさが300ピコメートル程度ということなので、非常に小さな測定が必要ということのようです)
そして、現状では、それに近い精度で測定が可能だというのですから、大きい数値だけでなく小さな数値についてもすごいことですね。
このように、宇宙に関係する数字はいろいろあるのですが、それらはスマホに入っている関数電卓アプリをつかって計算できます。 ぜひ、時間があるときにそれを使って遊んでみてください。きっと、自分の宇宙が頭の中に広がっていくでしょう。
現代は「数字で話す」必要があると言われていますが、このような数字は結構アバウトなのですが、それでもロマンを感じるでしょう。
(来歴)R2.10記事作成 R3.9題名変更 R3.12kyori1と合わせて全面書き直し R5.9月に誤字脱字見直し R6.8月見直し。 R7.10月確認