目では、太陽と月は同じぐらいの大きさに見えています。つまり、視直径がほぼ同じということですが、当たり前のような気もするし不思議な気もしませんか？
目視での太陽と月はどちらが大きく見えますか？
頭の中では、太陽の大きさはすごく大きくて、遠くにあるので小さく見えているということは誰もがイメージしているのですが、「満月の月」とどちらが大きく見えるのかとなるとどうでしょう？
太陽のほうがかなり大きいイメージがありませんか？
眼を細めて直接に見る太陽ではなくて、日食グラスで太陽を見たり、プラネタリウムで西に沈む太陽の大きさが意外に小さいなぁ … と思ったことはありませんか。
しかし、一方の「お月さん」も、沈む夕日と、ほどなくのぼってくる満月のお月さんを見ると、そんなに大きさが違っていません。どちらもよく似た大きさです。
月は楕円軌道を回っていて、地球から月までは 最遠距離で406,000km、最近距離で357,000kmと、月までの距離が約5万km変わるので、当然、地球から見える大きさが変わります。
PR
お月さんが大きく見えるスーパームーン
「スーパームーン」という言葉は最近しばしば聞くことがあるでしょう。
これは、一番地球に接近して、普段よりも大きく見えるときの「満月の月」をさす呼び方です。
このスーパームーンという言葉は占星術師が名付けたもので、天文用語ではないようですが、マスコミは何でもネタにするので、その言葉を気象予報士さんなどが言い出したことで急に広がり、WEBでも簡単に日時の情報が得られるようになりました。
スーパームーンと言われるのは、太陽と月と地球が並ぶ時（直列する時）、つまり、満月か新月のときですが、もちろん、新月のときは見えないので話題にはなりません。
また、満月以外のときの月の大きさも、地球との距離で変わっているのですが、満月のときには「意識してみることが多い」こともあって、それで「なんだか大きい感じがする」というイメージが定着してしまったのかもしれませんね。
非常に大きなスーパームーン（エクストラとかエクストリームをつけて呼ばれることもあるようですが）になるときにTVなどで大きく取り上げられて話題になります。
スーパームーンをバカチョンのズームで撮る
この写真は、2017年12月のスーパームーンをインスタントカメラのズームで撮ったのです。
これだけでは、大きさの違いわかりにくいのですが、下の写真のように、周囲の景色を入れて撮ったスーパームーンと普通の月の写真と合成して比較してみると、かなり大きさの違いを感じます。
スーパームーンの時には、視直径で15％程度おおきく、明るさで30％の差があると国立天文台のHPなどで説明されています。
月の大きさを写真合成して比較すると違いがわかる
この写真のように、空の真ん中に浮かんでいる月ではなく、建物のすぐ近くに月は、大きく見えるのですが、さらに、この写真は、家のベランダから、別の日に撮った月の写真を合成しているのですが、明らかに見えている大きさが違っていますね。
空に浮かぶ月は小さく見える
頭上の空に浮かぶ月は、背景に建物があるよりも、小さく見える感じがします。
これも、同じ写真から地上の風景を切り取っただけでも、背景がないと月が小さくなった感じになります。
月の出の大きく見える月も、頭上に浮かぶ月も、視直径は同じなのですが、見る人の頭が勝手に錯覚して、「月の出の地表近くに見える月は大きく見える」と判断しているようです。
PR
半月よりも満月は大きく見える？
半月などと比べて『満月は大きく見える』というイメージを持っている方も多いかもしれません。
しかし、これも、月と地球の距離できまることで、満月だから大きいと言うことではありません。
月が欠けていると目に入る光が少なくなるので、勝手に「満月は大きい」というイメージが頭に刷り込まれているのかもしれません。
平均視直径
この視直径について、理科年表には、「平均最近距離による視半径」として掲載されています。
理科年表の数字では、月は15分32秒、太陽は15分59秒なので、少しだけ太陽が大きいという数字になっていますが、この差では「ほぼ同じ大きさに見える」と言っていいかもしれません。
もう少し詳しい数字を比べてみましょう。
地球から月までの距離は最遠406,000km、最近357,000kmで、赤道半径が1,734.4kmで、最近接（スーパームーンの時）には視直径は15分59秒になります。つまり、このスーパームーンの時で、視直径は、太陽と同じくらいの大きさになります。
それで30％の明るさの差がでてくるようです。
PR
スーパームーンは18-19年周期ぐらいで起こるとされていますが
月は地球に同じ面を向けているので、地球の自転と月の公転は同じで、月の地球に対する公転周期は約27.3日で、そして、地球が太陽に対して公転していますが、月の軌道は太陽や地球の引力の影響でふらついています。
満月から満月まで（これを朔望といいます）の周期は約29.5日で、その間に1回、月は地球に近づいたり離れたりしています。
それらによって、同じ「満月」でも大きさが違うと言うことになります。
国立天文台のHPを見ると、視直径の最大最小が半年程度ごとに繰り返しているグラフが掲載されています。（この国立天文台HP記事は興味深い内容が多いので、ぜひご覧ください）
つまり、スーパームーンの定義もきっちりしていないので、大きさにこだわらなければ毎年1回程度は、かなり地球に近づく場合があって、お月さんが結構大きく見えるときがあります。
しかし、本当に最大に見えるスーパームーンはそんなにないはずですが、毎年のように「今年の＊＊の満月はスーパームーンです」などとTVなどで言われています。
 |
SKISUNO 天文学 模型 教育 道具 太陽 システム 模型 装飾 模型 天文 器具 地理 教育 装置 太陽 地球 と 月 模型 教室 装置 新品価格 |
天体の明るさの雑学
太陽の極大等級（明るさ）は－26.8等級とされています。それに対して、月は－12.9等級。
全天で最も明るく輝く「おおいぬ座のシリウス」は－1.5等級で、明るさが1等級変わると2.5倍明るくなると決められているので、5等級変わると約100倍（すなわち2.5の5乗 2.55 ≒98）の明るさの違いになります。
全天で最も明るい恒星の、冬の季節にオリオン座の近くに明るく見える「シリウス」との明るさの違いを関数電卓で計算してみると、月はシリウスの34000倍、太陽は月の約340000倍です。
太陽はシリウスの約117億倍明るいと計算できます。
【参考】天体の話にでてくる数字は、大きいものが多いのですが、関数電卓は、難なくそれを表示してくれます。
そして、自分で計算してみると、親密さが増します。関数電卓の使い方はムズがしいものではないので、これを機会に、少し使う練習をしてみましょう！
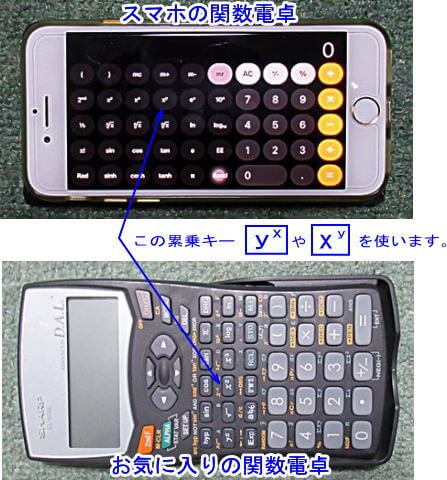
今はスマホのアプリで「関数電卓」が入っているので便利なのですね。 関数キーは慣れないと使いにくいので、上のアイフォンアプリの例を簡単に紹介します。
私の使っているi-phoneの電卓アプリは、縦画面が普通電卓で横画面にすると関数電卓になります。
上の例で言えば、シリウスは-1.5等級、太陽は-26.8等級なので、その差は25.3等級（-1.5-（-26.8）＝25.3）なので、関数電卓の「累乗キー」を使って、2.5［累乗キー］25.3［累乗キー］を順に押すと、すごい数字の答えがでますが、ここでは、すごい大きな数字だというところだけを見ておいてください。
2等星の北極星と太陽の等級差は 2-（-26.8）＝28.8 です。 上に5等級差が約100倍と書きました。 これは 2.5［累乗キー］5［累乗キー］で 97.65・・・となるのを、関数電卓で確認できますね。
練習してみましょう。 ＊＊＊＊＊
ともかくこのように、星に対しては、月も太陽も明るすぎる異端児なのですが、視直径で同じぐらいの月と太陽が地球の周りに付き添って回ってくれていることで、今の私たちが地球に住んでいられるのですから、太陽も月も、信仰の対象になって、神様として崇められるのは当然でしょうね。
近くて遠い月
アポロ宇宙船が月へ行ったのは1969年で、当時のケネディー大統領の公言で実現したのですが、そのアポロ11号は、地球発射から月面到達までの時間は 102時間 45分、月面離陸から地球帰還までは 70時間55分かかっています。
月までの距離は約38万kmです。
光は毎秒30万km進むので、2秒かからずに月まで行ってしまうのですが、人間が行くとなると、その18万倍以上の時間がかかっていることになります。
このように、電卓で計算してみると、実感の仕方が変わってきます。ぜひ計算してそれを実感してみてください。
さいごに：ここにある数字等は、主に国立天文台編集の理科年表をもとにして拙い計算した数字で、記事中の写真はすべて家の近くでインスタントカメラで撮ったものです。特に検証もしていませんので、雑学としてお読みください。
（来歴）R5.2月に誤字脱字を合わせて見直し R6.11月確認